Regular maps in the orientable surface of genus 0

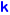
NameSchläfliV / F / EmV, mFnotes C&D no.imageswire-
frames
the tetrahedron{3,3}44 / 4 / 6 1,1 replete singular is a polyhedral map permutes its vertices evenly R0.110
the cube{4,3}68 / 6 / 12 1,1 replete singular is a polyhedral map permutes its vertices evenly R0.2′10
the octahedron{3,4}66 / 8 / 12 1,1 replete singular is a polyhedral map permutes its vertices oddly R0.210
the dodecahedron{5,3}1020 / 12 / 30 1,1 replete singular is a polyhedral map permutes its vertices evenly R0.3′10
the icosahedron{3,5}1012 / 20 / 30 1,1 replete singular is a polyhedral map permutes its vertices evenly R0.310
the 1-hosohedron{2,1}22 / 1 / 1 1,2series i Vertices with < 3 edges Faces with < 3 edges Faces share edges with themselves trivial is not a polyhedral map permutes its vertices oddly R0.n110
the dimonogon{1,2}21 / 2 / 1 2,1series z Vertices with < 3 edges Faces with < 3 edges Vertices share edges with themselves trivial is not a polyhedral map permutes its vertices evenly R0.n1′20
the 2-hosohedron{2,2}22 / 2 / 2 2,2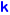series k Faces with < 3 edges Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n22 4
the di-triangle{3,2}63 / 2 / 3 1,3 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n3′20
the 3-hosohedron{2,3}62 / 3 / 3 3,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n320
the di-square{4,2}44 / 2 / 4 1,4series m Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n4′2 4
the 4-hosohedron{2,4}42 / 4 / 4 4,1series l Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n44 4
the di-pentagon{5,2}105 / 2 / 5 1,5 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices evenly R0.n5′10
the 5-hosohedron{2,5}102 / 5 / 5 5,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n520
the di-hexagon{6,2}66 / 2 / 6 1,6 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n6′10
the 6-hosohedron{2,6}62 / 6 / 6 6,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n620
the di-heptagon{7,2}147 / 2 / 7 1,7 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n7′10
the 7-hosohedron{2,7}142 / 7 / 7 7,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n720
the di-octagon{8,2}88 / 2 / 8 1,8 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n8′10
the 8-hosohedron{2,8}82 / 8 / 8 8,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n820
the di-nonagon{9,2}189 / 2 / 9 1,9 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices evenly R0.n9′10
the 9-hosohedron{2,9}182 / 9 / 9 9,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n920
the di-decagon{10,2}1010 / 2 / 10 1,10 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n10′10
the 10-hosohedron{2,10}102 / 10 / 10 10,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n1020
the di-11-gon{11,2}2211 / 2 / 11 1,11 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n11′10
the 11-hosohedron{2,11}222 / 11 / 11 11,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n1120
the di-dodecagon{12,2}1212 / 2 / 12 1,12 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n12′10
the 12-hosohedron{2,12}122 / 12 / 12 12,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n1220
the di-13gon{13,2}2613 / 2 / 13 1,13 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices evenly R0.n13′10
the 13-hosohedron{2,13}262 / 13 / 13 13,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n1320
the di-14gon{14,2}1414 / 2 / 14 1,14 Vertices with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n14′10
the 14-hosohedron{2,14}142 / 14 / 14 14,1 Faces with < 3 edges trivial is not a polyhedral map permutes its vertices oddly R0.n1420
the edgeless map{0,0}1 / 1 / 0 0,0series s Vertices with < 3 edges Faces with < 3 edges is not a polyhedral map trivial permutes its vertices evenly R0.010

Other Regular Maps

General Index

Orientable
sphere | torus | 2 | 3 | 4 | 5 | 6 |
Non-orientable
projective plane | 4 | 5 | 6 | 7 |