The letter is followed by an integer denoting the genus, then a dot, then an arbitrarily-assigned integer, and finally, in the case of dual pairs, a prime to indicate the member of the pair with larger faces. Thus what I have called S3:{7,3} has the C&D identifier R3.1'.
These identifiers have the huge advantage that they are unique. Other naming systems for regular maps lack uniqueness, see Schläfli symbol below.
It is of interest to us because the uniform cantellation of a self-dual regular map yields another regular map. Each vertex becomes a face, each face remains a face, and each edge becomes a vertex. If the original was {p,p} with q vertices, q faces and pq/2 edges, then the new regular map is {p,4} with pq/2 vertices, 2q faces, and pq edges. It is still in the same manifold.
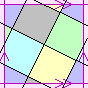chiralA chiral regular map in the torus is shown to the right.
A chiral object's full symmetry group is the same as its rotational symmetry group; a non-chiral object's full symmetry group is twice the size of its rotational symmetry group.
degenerateDuality is a symmetric relation: if A is the dual of B then B is the dual of A, hence the name.
An Eulerian circuit is one which traverses every edge of a graph exactly once, ending on the vertex where it started.
A double-Eulerian circuit is one which traverses every edge of a graph exactly once in each direction, ending on the vertex where it started.
See also Hamiltonian.
A polyhedron or other regular map has four flags for each edge.
In these pages, the genus of an orientable surface may be designated by Sn, with the sphere being S0, the torus S1, etc.; and that of a non-orientable surface by Cn, with the projective plane being C1, the Klein bottle C2, etc.
The genus of a group is the least genus of any manifold on which its Cayley diagram can be drawn without the arcs crossing.
A regular map is edge-transitive if any edge can be mapped to any other edge. It is half-edge-transitive if any edge can be mapped to any other edge with the edge either way round.
A Hamiltonian circuit is one which visits every vertex of a graph exactly once, using no edge more than once, and ending on the vertex where it started.
A double (n-fold) Hamiltonian circuit is one which visits every vertex of a graph exactly twice (n times), using no edge more than once, and ending on the vertex where it started.
See also Eulerian.
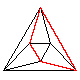holeAn octahedron with a hole highlighted in red is shown to the right.
See also Petrie polygon.
pathologicalPetrie duality is a symmetric relation: if A is the Petrie dual of B then B is the Petrie dual of A. Also, the Petrie dual of the dual of the Petrie dual is the dual of the Petrie dual of the dual.
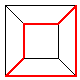Petrie polygonIf you have embedded the structure in 3-space, you will find that its Petrie polygons are skew.
The concept of holes and Petrie polygons can be generalised, as described in holes and Petrie polygons.
In every genus where I have identified the regular maps, the highest quality is a multiple of 3. I expect there is a simple reason for this.
A Schläfli symbol can specify a stellated polyhedron, by using non-integers. {5/2,5} is the small stellated dodecahedron, with five pentagrams meeting at each vertex, and {3,5/2} is the great icosahedron, with "two-and-a-half" triangles meeting at each vertex, i.e. its vertex figures are pentagrammal. Stellated polyhedra are not considered in these pages.
This can be extended to polytopes. The Schläfli symbol for the 600-cell is {3,3,5}. The 3,3 specifies tetrahedron; the 5 specifies that 3 of these meet at each edge. But in these pages we are only concerned with polyhedra, having two main numbers in the Schläfli symbol.
If we are only concerned with genus-0 regular maps (regular polyhedra), a simple Schläfli symbol of the form {G,H} is sufficient to specify a polyhedron. But if we look more broadly, more numbers may be used, to disambiguate. Here are some examples.
- {4,6|4} specifies a polyhedron with six squares meeting at each vertex. The 4 after the | specifies that its holes have four edges. This is an infinite polyhedron of infinite genus: it can be seen in the first picture in the Wikipedia article Regular skew polyhedron.
- {7,3}8 specifies a regular map with three heptagons meeting at each vertex. The single subscript 8 specifies that its Petrie polygons have eight edges. We have a picture of {7,3}8, it has genus 3.
- {6,3}(2,0) specifies a regular map with three hexagons meeting at each vertex. There are infinitely many regular maps designated by {6,3}, all of genus 1. The bracketed two-number subscripts specifies one of these. Unfortunately I use a notation different from that used by ARM, although we both use bracketed two-number subscripts: the difference is explained in the page Regular Maps on the Torus.
However, these various enhancements to Schläfli symbols are not enough to make them unambiguous. {8,8|4}2 and {8,8|4}2 are different regular maps, of genus 2 and 3 respectively, the latter being the double cover of the former.
Therefore in these pages I disambiguate Schläfli symbols with a prefix to indicate the genus where necessary. E.g. I will designate those two polyhedra as S2:{8,8} and S3:{8,8}. Where I omit the prefix it should be clear from the context.
Thus a map is said to be face-transitive if, for any two faces a, b there is some operation of its symmetry group which maps a to b. Likewise for vertex-transitive, edge-transitive, half-edge-transitive, flag-transitive, etc.