The Cayley diagram above, drawn on a surface of genus 2, portrays the only group which is of genus 2 (i.e. its Cayley diagram can be drawn, without crossings, on a surface of genus 2 but not on one of genus 1).
The pink arrows around the edge of the diagram, and the letters in the two round light pink regions, are "sewing instructions". To convert this flat image to a genus-2 surface, we must cut away and discard the light pink regions, and join up the cut edges as indicated by the pink arrows.
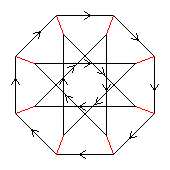
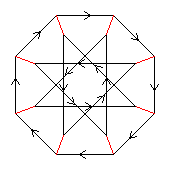
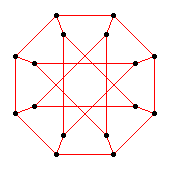
The two Cayley diagrams to the right portray the quasidihedral and modular groups of order 16. If we ignore their colouring and remove their arrows, we get the graph to the left. This is the Möbius–Kantor graph, an example of a generalised Petersen graph. This Möbius–Kantor graph has 16*3! = 96 automorphisms, which form a group. This group is "Tucker's Genus 2 Group", as potrayed by the big Cayley diagram above.
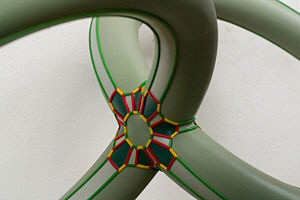
The same Cayley diagram is the subject of a sculpture by DeWitt Godfrey and Duane Martinez. A detail (the interesting bit in the middle) is shown to the right — there is a larger version in Wikipedia. It is not clear from this detail how the green lines that go the long way round the loops join up — but this can be established from the page "Art and mathematics blended into interesting collaborative project", which shows a prototype of the sculpture, and the complete sculpture, both making it clear how those lines twist around.
Thus the image to the right is not computer-generated. It is a photograph of a sculpture, a physical object weighing 50 lbs (23kg). This sculpture is in the Technical Museum of Slovenia, Chateau Bistra, Borovnica, Slovenia.
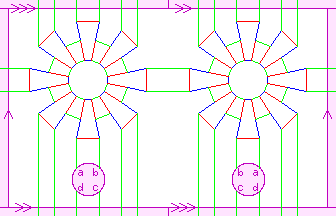
To the left is another, less pleasing, portrayal of the same group.
Where the sculpture has yellow lines, my diagrams above and left have blue lines, for the sake of visibility on a white ground.
The group is named after Thomas Tucker, Professor of Mathematics at Colgate University, who in 1983 showed that it is the only group of genus 2, in his paper There is one group of genus two.
Some more Cayley diagrams drawn on the genus-2 surface (though they could have been drawn on a surface of lower genus).
Some regular maps drawn on the genus-2 surface.
Some more Cayley diagrams drawn on surfaces appropriate to their genus.
Some more Cayley diagrams
and other pages on groups
Copyright N.S.Wedd 2009