This page is obsolete. See the current version of Regular Maps in the orientable surface of genus 3

Regular Maps on the Genus-3 Orientable Manifold

This page shows some of the regular maps that can be drawn on the genus-3 orientable manifold. For the purpose of these pages, a "regular map" is defined here.

To draw these maps, we need a way of portraying the oriented genus-3 surface in 2-space. We may use any of the diagrams shown to the right, among others. The surface itself is shown in white, the pink letters show how the "cut edges" are to be joined up, and the light pink regions are not part of the surface. This is further explained by the page Representation of 2-manifolds.

The first portrayal of the genus-3 surface can be regarded as a cube, with a tunnel drilled between each pair of opposite faces.

The first two columns in the main table below were created by listing every possible polyhedron {G,H} with V vertices F faces and E edges which would have Euler number -4. The last column states that such a map actually exists, or links to a proof that none does, if I know either.

An image in the "thumbnail" column of the main table is a link to a page with more information about the regular map. Where the thumbnail image is shown on a grey background, the link is to a map that is not regular.

Schläfli symbol C&D no.	V+F-E=Eu	thumbnail (link)	dual Petrie dual	Rotational Symmetry Group	comments	qy
{7,3} R3.1′	56+24-84=-4		{3,7} C9{8,3}	PSL(2,7)	Pyritification of {14,3} below.	12
{3,7} R3.1	24+56-84=-4		{7,3} C41{7,8}
{8,3} R3.2′	32+12-48=-4		{3,8} S1{6,3}(4,4)	A group of order 96		6
{3,8} R3.2	12+32-48=-4		{8,3} S11?: {6,8}
{6,4} R3.4′	12+8-24=-4		{4,6}	A group of order 48		4
{4,6} R3.4	8+12-24=-4		{6,4}
{12,3} R3.3′	16+4-24=-4		{3,12} S2{8,3}	GL(2,3)		2
{3,12} R3.3	4+16-24=-4		{12,3} S8?: {8,12}
{8,4} R3.6′	8+4-16=-4		{4,8} self-Petrie dual?	A group of order 32	Can be obtained by cantellation of {8,8}2 below.	2
{4,8} R3.6	4+8-16=-4		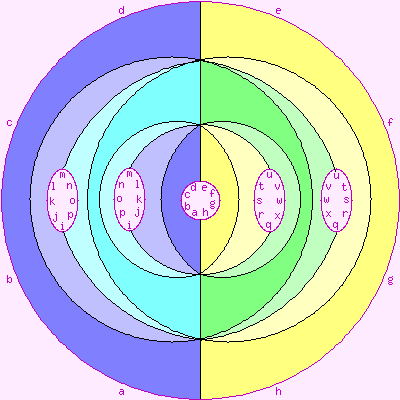{8,4} S5:{8,8}
{8,4} R3.5′	8+4-16=-4		{4,8} self-Petrie dual?	A group of order 32	Can be obtained by cantellation of {8,8}4 below.	2
{4,8} R3.5	4+8-16=-4		{8,4}
{6,6} R3.8	4+4-12=-4		self-dual S2{4,6}	S4		2
{8,8}4 R3.10	2+2-8=-4		self-dual S2{4,8}	Modular of order 16		1
{8,8}2 R3.11	2+2-8=-4		self-dual 8-hosohedron	C8×C2		1
{12,4} R3.7′	6+2-12=-4		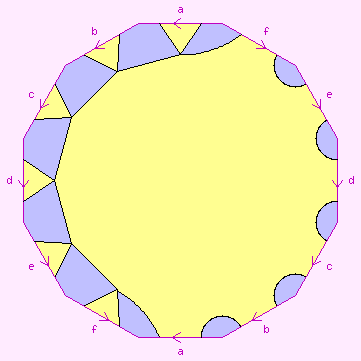{4,12} S2{6,4}	D24		1
{4,12} R3.7	2+6-12=-4		{12,4} S4?: {6,12}
{12,12} R3.12	1+1-6=-4		self-dual 6-hemihosohedron	D12		½
{14,7} R3.9′	2+1-7=-4		{7,14} 7-hosohedron	D14		½
{7,14} R3.9	1+2-7=-4		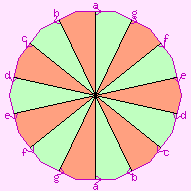{14,7} 7-hemihosohedron

Maps that do not have a regular form

Where the table below has a thumbnail image linking to a page, it is about an irregular map. Its faces all have the same number of edges, as do its vertices; but it is not half-edge transitive.

Schläfli symbol	V+F-E=Eu	thumbnail (link)	dual	Evidence for non-existence, other comments
{9,3}	24+8-36=-4		{3,9}	∄ With eight nonagons, for transitivity each face must border three of the others three times each. This imposes enough constraints that I do not believe a regular polyhedron exists. The faces of {7,3} can be fused in threes to make a {9,3} which is not regular.
{3,9}	8+24-36=-4		{9,3}
{10,3}	20+6-30=-4		{3,10}	∄: D C6{10,3}5 and C6{10,3}10 both exist.
{3,10}	6+20-30=-4		{10,3}
{14,3}	14+3-21=-4		{3,14} S1{6,3}(1,3)	Can be pyritified to produce {7,3} above. {14,3} is the Heawood graph
{3,14}	3+14-21=-4		{14,3}
{18,3}	12+2-18=-4		{3,18}	∄: D
{3,18}	2+12-18=-4		{18,3}
{30,3}	10+1-15=-4		{3,30}	∄ If this existed, there would be a regular double-Eulerian circuit of the hemi-dodecahedron.
{3,30}	1+10-15=-4		{30,3}
{5,4}	20+16-40=-4		{4,5}	∄: S5
{4,5}	16+20-40=-4		{5,4}
{20,4}	5+1-10=-4		{4,20}	∄ S3:{20,4} does not exist. C6:{20,4} does.
{4,20}	1+5-10=-4		{20,4}
{6,5}	6+5-15=-4		{5,6}	∄: S5, another proof
{5,6}	5+6-15=-4		{6,5}
{10,5}	4+2-10=-4		{5,10}	∄: E
{5,10}	2+4-10=-4		{10,5}
{9,6}	3+2-9=-4		{6,9}	∄: S3
{6,9}	2+3-9=-4		{9,6}
{5,5}	8+8-20=-4		self-dual	∄: S5