This is a sub-page of How to Build Groups.

How to Build Groups: Toll-bean Extensions

Introduction

I assume that the reader is familiar with Cayley diagrams. For some Cayley diagrams, as used in these pages, see Cayley Diagrams of Small Groups, which gives one or more Cayley diagrams for every group of order less than 32. The Cayley diagrams on all these pages,and in general, have the following properties:

There is one colour of arc corresponding to each generator.
There is one vertex of the diagram corresponding to each element of the group.
Generators of period 2 correspond to arcs without arrows, that may be traversed in either direction; generators of period greater than 2 correspond to arcs with arrows, that may be traversed only in the direction of the arrow.
At each vertex, there is one incoming arc and one outgoing arc of each colour. For arrowed arcs, these are distinct; for period-2 arcs these are the same one.


Fig. 2
A toll station on an arc with an arrow


Fig. 1
A toll station on an arc with no arrow

We will now extend these diagrams by adding "toll stations", orange triangles, to them.

An arc like the one in Fig. 1 has a toll station, but no arrow. As there is no arrow, this arc can be traversed in either direction – until the addition of the toll station, it represented an element of period 2. Now with the presence of the toll station, if you traverse it from left to right, you collect a toll bean. If you traverse if from right to left, you don't collect a toll bean.

An arc like the one in Fig. 2 has a toll station, and an arrow. If you traverse it from left to right, you collect a toll bean. You may not traverse if from right to left.

The beans themselves form a group. In all the examples presented on this page, they form a cyclic group: so if the order of this "bean group" is n, once you have collected n beans, you throw them all away. In general though, if there are several kinds of toll station, handing out several kinds of bean, you need to keep the beans of different kinds separate, and throw away a set of beans of one kind when it reaches the size specified for that colour. (You can ignore the order in which you receive them: the "bean group" can be proved to be Abelian.)

If only one kind of toll station appears in the diagram, there is only one kind of bean, and the beans necessarily form a cyclic group – this will be the case for all of the groups discussed on this page. The size of the bean group is indicated by an orange number in the upper right corner of the diagram.

Some examples.


C1

C1

This is not helpful. There is no arc on which to put a toll station.


C2

C2

There is only one way to add a toll station to this Cayley diagram of C2. We can choose the size of the cyclic group generated by the beans: we will try 2 and 3.


Fig. 3

Fig. 3 is a Cayley diagram for a group with four elements: you can be at either end of the arc, and you can have zero or one beans. The group's generator has period 4, so this group must be C4.


Fig. 4

Fig. 4 is a Cayley diagram for a group with six elements: you can be at either end of the arc, and you can have zero, one or two beans. The group's generator has period 6, so this group must be C6.

This is not very interesting, so far. We have only built cyclic groups, which we already knew about.


C3

C3

There are three ways to add at least one toll station to this Cayley diagram of C3. We can also choose the size of the cyclic group generated by the beans: we will try 2 and 3.


Fig. 5


Fig. 6


Fig. 7


Fig. 8


Fig. 9


Fig. 10

Fig. 5 is a Cayley diagram for a group with six elements: you can be at any corner of the triangle, and you can have zero or one beans. This is C6 again.

Fig. 6 turns out to have only three elements, there is no way to get back to your starting position with a bean. This is just C3.

Fig. 7 is in effect equivalent to Fig. 5.

Fig. 8 is a Cayley diagram for a group with nine elements: you can be at any corner of the triangle, and you can have zero, one or two beans. This is C9.

Fig. 9 is in effect equivalent to Fig. 8.

Fig. 10 is similar in effect equivalent to Fig. 6, it is just C3.

This is still not very interesting. But we have achieved something that we couldn't do with direct and semidirect products: Fig. 4 gave us C4, and Fig. 8 (and 9) gave us C9. We can now use toll stations to build prime-squared cyclic groups from prime groups.


C4

C4

There are several ways to add toll stations to this Cayley diagram of C4. We will consider only one of them, and will use beans that generate C2.


Fig. 11

Fig. 11 generates a group with eight elements. Its generator has period 8, so this group is C8.

This is included to show how we can not only build prime-squared cyclic groups from prime cyclic groups, but can repeat the process to build all prime-power cyclic groups from them.

Our starting material used to be all cyclic groups. Now we know how to build all prime-power cyclic groups from prime cyclic groups, and then all cyclic groups as direct products of those. So we only need the prime cyclic groups as our starting material, and we are hoping to be able to build all solvable groups from them.


C2×C2

C2×C2

Now things start to get more interesting.

Excluding ways which are very obviously related to others by symmetry, there are twelve ways to add toll stations to C2×C2. We shall consider all of them, but only the versions where the beans generate C2.


Fig. 12


Fig. 13


Fig. 14


Fig. 15


Fig. 16


Fig. 17


Fig. 18


Fig. 19


Fig. 20


Fig. 21


Fig. 22


Fig. 23

Some of these diagrams are invalid. These are indicated by a grey background, and will be disregarded.

See sub-page on valid and invalid Cayley diagrams.

In Fig. 13, denoting the generators by k (black) and r (red), we see that k⁴=1, r²=1, krkr=1. This is D8.
In Fig. 14, similarly, we see that k⁴=1, r²=1, krkr=k². This is C4×C2.
In Fig. 21 we see that k⁴=1, r⁴=1, krkr=1. This is C4×C2 again.
In Fig. 22 we see that k⁴=1, r⁴=1, krkr=k². This is Q8.
In Fig. 23 we see that k⁴=1, r⁴=1, krkr=1. This is C4×C2 again.

So we have managed to build Q8 by this method. If we can build Q8, we can build another three of the 93 groups of order less than 32, specifically, Q8×C2, Q8×C3, and Q8⋊C3 ≅ SL(2,3). The only group of order less than 32 than we still cannot build is Q16; and we will see how to build Q16 further down the page.

Advice on placing toll stations

We can learn from these invalid diagrams how to avoid drawing invalid diagrams. We can see that if any arc of some colour has a toll station but no arrow, all arcs of that colour must have toll stations. This is in fact easy to prove: if there are two arcs corresponding to some generator x which (without the toll stations) would have period 2, one with a toll station and one without, then starting at the end of one arc we find that x still has period 2, while starting at the end of the other its period is now 4.


C2×C2

C2×C2 again

Now we will treat C2×C2 as having three generators, and the presentation < r,g,b | r², g², b², rgrg, gbgb, brbr, rgb >.

Excluding ways which are related by symmetry, there are four ways to add toll stations to this tetrahedral Cayley diagram of C2×C2.


Fig. 24


Fig. 25


Fig. 26


Fig. 27

In Fig. 24, denoting the generators by r (red), g (green), and b (blue), we see that r⁴=1, g⁴=1, b⁴=1, (rgb)⁴=1, (rbg)²=1. This is Q8.

In Fig. 25, we see that from the bottom left, (rgb)²=1; but from the bottom right, (rgb)²≠1, (rgb)⁴=1. This is not a valid diagram, so it is shown with a grey background.

Fig. 26 is invalid, for a similar reason to Fig. 25.

Fig. 27, like Fig. 24, portrays Q8.

Note that Fig. 27 is Fig. 24 with all six toll stations reversed. In general, if you take a valid Cayley diagram, choose a set of colours each corresponding to elements of period two, and reverse all the toll stations on arcs of those colours, you still have a valid Cayley diagram and it portrays the same group. Proof: if the elements portrayed by these arcs of period two are i, j, etc., then by mapping i↔i³, j↔j³, etc., we reverse all those toll stations while leaving the group unaffected. We can use this rule to reduce the number of diagrams we need to consider.


D12


D10


D8


D6

Dihedral groups

Now we will consider dihedral groups, and add toll stations in various ways. We can add them to the spokes, or add one to the rim, or both. If the order of the dihedral group is a multiple of 4, we can arrange the toll stations on the spokes all to run inwards, or to run alternately inwards and outwards.


Fig. 28


Fig. 29


Fig. 30


Fig. 31

In Fig. 28, denoting the generators by r (red) and k (black), we see that k³=1, r⁴=1, rk=k²r. This is C3⋊C4, which is isomorphic to Dic12 also known as Q12. We have expanded the two-cycles to four-cycles.

In Fig. 29, k⁴=1, r⁴=1, rk=k³r. This is C4⋊C4, which is not Q16. Again we have expanded the two-cycles to four-cycles.

Fig. 30 portrays C5⋊C4, ≅ Dic20 or Q20.

Fig. 31 portrays Dic12×C2, ≅ C6⋊_C2C4. This is not Q24.


Fig. 32


Fig. 33

Fig. 32 portrays a group whose elements have the orders 1.2⁷.4⁸, and with the centre { 1,k²,r²,k²r²} ≅ C2×C2. This is (C2×C2)⋊C4.

Fig. 33 portrays a group whose elements have the orders 1.2.4¹⁰.8⁴. This is C3⋊D8.


Fig. 34


Fig. 35


Fig. 36


Fig. 37

In Figures 34, 35, 36, and 37 the toll stations have doubled the lengths of the cycles, but the dihedral structure is not affected. These figures portray D12, D16, D20 and D24 repectively.


Fig. 38


Fig. 39

Fig. 38 portrays a group with elements of orders 1.2.3².4⁶.6². This is Dic12, also called Q12, and is isomorphic to C3⋊C4.

Fig. 39 portrays a group with elements of orders 1.2.3².4⁶.6². This is Q16. It is not isomorphic to C4⋊C4; unlike C4⋊C4, it has elements of order 8.


Fig. 40


Fig. 41

Fig. 40 portrays a group with elements of orders 1.2.4¹⁰.5⁴.10⁴. This is Dic20, also called Q20, and is isomorphic to C5⋊_C2C4.

Fig. 41 portrays a group with elements of orders 1.2.3².4¹⁴.6².12⁴. This is Q24. It is not isomorphic to C6⋊C4.


Fig. 42


Fig. 43

Fig. 42 portrays a group with elements of orders 1.2⁵.4⁶.8⁴. This is the quasidihedral group of order 16.

Fig. 43 portrays a group with elements of orders 1.2⁹.3².4⁶.6⁶. It is isomorphic to C3×D8.


Fig. 44

We now have a general method for building dicyclic groups, including Q16, from dihedral groups. We ought to be able to build Q8 from D4, if there were such a group as D4. If we accept that D4 is a way of describing C2×C2, we can see how to do this by looking at Fig. 22, or at Fig. 44 which is a re-coloured and re-oriented version of Fig. 22.


A4

A4

Now we consider A4, which is isomorphic to the tetrahedral group.

If we are to put the toll stations on the period-2 generator, Fig. 24 above gives a hint as to how to orient them so as to produce a valid Cayley diagram.

If we are to put them on the period-3 generator, we want to arrange

one on each three-cycle
one bordering each (kr)³ hexagon. There is (up to symmetry) a unique way to do this.


Fig. 45


Fig. 46

In Fig. 45, we see that k³=1, r⁴=1, and (kr)³=1. This is SL(2,3), which is isomorphic to the binary tetrahedral group, and to Q8⋊C3.

Fig. 46 portrays a 36-element group that can be presented as < k,r | k³, r⁴, (kr)⁹ >.


Fig. 47


Fig. 48

Fig. 47 portrays A4×C2.

Fig. 48 portrays a 36-element group that can be presented as < a,b,t | a², b², t⁹, ab=ba, ta=bt, tb=abt >.


S4 (trunc. octahedron)


S4 (truncated cube)

S4

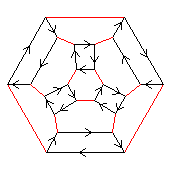
Now we consider S4, which is isomorphic to the octahedral group.

We can start with either of the Cayley diagrams shown. They both portray the same group and have the same symmetry. There are numerous ways we can add toll stations to them; four of these are shown below.


Fig. 49

Fig. 49 has the toll stations placed in most obvious way. They do not affect the 4-cycle generated by k, so no 8-cycles are generated that way. However they extend the 3-cycles generated by (kr) and by (rk) to 6-cycles. The periods of the elements of the group portrayed by figure 49 are 1.2¹⁹.3⁸.4¹².6⁸. This is S4×C2, its central element is (k²r)².


Fig. 50

Fig. 50 has toll stations placed on the elements of period 2, in such a way that two of the eight hexagons have all three running anticlockwise and six of them have two running clockwise and one running anticlockwise. This gives a group whose elements have periods 1.2⁷.3⁸.4²⁴.6⁸. It is A4⋊C4.

There are other ways of arranging the toll stations on the red arcs so as to produce a valid Cayley diagram. Disappointingly, I have failed to find one which creates the binary octahedral group.


Fig. 51

Fig. 51 has toll stations placed on the elements of period 2 in such a way that their directions alternate as one goes around each octagon. This also gives a group whose elements have periods 1.2⁷.3⁸.4²⁴.6⁸. It is A4⋊C4 again.


Fig. 52

Fig. 52 has toll stations placed as irregularly as possible while keeping the diagram valid. Three of the octagons have three clockwise toll stations and one anticlockwise, and the other three have the opposite. This gives a group whose elements have periods 1.2.3⁸.4¹⁸.6⁸.8¹². This is the binary octahedral group: it has Q16 as a subgroup, generated by kr and k²rk.


A5

A5

Finally we consider A5, which is isomorphic to the icosahedral group.

An easy way to add toll stations while ensuring that the diagram remains valid is to put them on all the black arcs. This gives rise to Fig. 51.

Adding toll stations to the red arcs, while maintaining a valid Cayley diagram, is not so easy. All the hexagons must have the same number, modulo 2, of toll stations pointing anticlockwise as we go round them. This number is wlog 0. But the mean number of toll stations pointing anticlockwise must also be 0. So, of the 20 hexagonal faces, 5 must have 0 anticlockwise-oriented toll stations and 15 must have 2. These 5 all-clockwise hexagons must be distributed fairly even over the icosahedron, which must destroy most of the symmetry of the diagram. It turns out that this can nevertheless be achieved while maintaining a valid Cayley diagram. The result is Fig. 54.


Fig. 53

Fig. 53 has {1, k⁵} as a central subgroup. We can reach any vertex with no beans, by taking any route but replacing k by k⁶ and k³ by k⁸. So Fig. 51 portrays A5×C2, also known as the "full icosahedral group". Where A5 is the symmetry group of an icosahedron under rotation, A5×C2 is the symmetry group of an icosahedron under rotation and reflection, with the central element being inversion through the centre. It has no element of period 4: the periods of its elements are 1.2³¹.3²⁰.5²⁴.6²⁰.10²⁴.


Fig. 54

Fig. 54 is more interesting. It has only one element of period 2, and 30 of period 4, with the periods of the elements being as for A5×C2 but with all but one of the 2s replaced by 4s: 1.2.3²⁰.4³⁰.5²⁴.6²⁰.10²⁴. This is the "binary icosahedral group". It is isomorphic to SL(2,5), A5 being isomorphic to PSL(2,5).

Both groups are distinct from S5, whose elements have periods 1.2¹⁵⁺¹⁰.3²⁰.4³⁰.5²⁴.6²⁰.

Summary

Now that we can build direct products, semidirect products, and toll-bean extensions, we can, starting only from prime cyclic groups, build all 93 groups of order less than 32.

Moreover, we can build the five sets of "binary polyhedral" groups.

"Binary cyclic groups" are even cyclic groups, built as in Fig. 3 and Fig. 5.
"Binary dihedral groups" are dicyclic groups, built as in Fig. 38, Fig. 39, Fig. 40 and Fig. 41.
The "binary tetrahedral group" is built as in Fig. 45.
The "binary octahedral group" is built as in Fig. 52.
The "binary icosahedral group" is built as in Fig. 54.

Theory

The group generated by the beans alone forms a normal subgroup of the group portrayed by the whole Cayley diagram. Proof: Let xyz denote an arbitrary sequence of generators. After traversing the diagram according to xyz, we arrive at some vertex v with some number of beans. If we then reverse the process, traversing the diagram according to (xyz)^-1, we arrive back where we started, with some number of beans. If at v we had been given some number n of beans, we would still arrive back where we had started with some (possibly different) number m of beans. So we have (xyz) bⁿ (xyz)^-1 = b^m. So the group generated by b is a normal subgroup of the whole group.

The quotient group is (isomorphic to) the group portrayed by the Cayley diagram ignoring the toll stations.

If there is only one kind of toll station, the group generated by the beans must be cyclic.

If there is more than one kind of toll station, they may pay out different kinds of beans. These beans may commute, or may interact, i.e. not commute. For instance, if one type of toll station pays out orange beans of period 3, and another pays out pink beans of period 2, the beans might generate < o,p | o³=1, p²=1, po=o²p > which is D6. If the beans generate a non-Abelian group like this, it is important to keep them in order as you receive them. I now believe that this can't happen. The bean group must be Abelian.

If the beans generate a cyclic, or other Abelian, group, this group is in the centre of the group portrayed by the whole Cayley diagram. Proof: Any element of the group takes you from your starting vertex p to some vertex q while acquiring element b of the bean group. Its inverse x^-1 must take you from q to p while acquiring element b^-1 of the bean group. So, if a is some other element of the bean group, xax^-1a^-1 takes you from p to q while acquiring element b of the bean group, then you acquire element a of the bean group, then you return to p while acquiring b^-1, then you acquire a^-1. Finally you are back where you started with element bab^-1a^-1; but the bean group is Abelian, so you are back where you started with no bean. So xax^-1a^-1 must equal the identity for all x and a, and the bean group is central. All the groups built on this page have Abelian (indeed cyclic) bean groups, which form the centres of the extended groups.

How do "Toll Beans" relate to conventional treatments of group extensions?

The usual treatment goes like this. A group G has a normal subgroup N and a quotient group H. Regard H as the group of the cosets of G. Pick a "factor set": a representative from each coset, with the one from the identity of the quotient group being the identity of G. Find a map from H×H to N such that the factor set is "compatible", i.e. everything fits together right

Using toll stations and toll beans, it is easier than this. Instead of having H×H, that is two whole copies of H, to juggle, we just have H×{the generators of H}. The H is the unadorned Cayley diagram, and the set of its generators is the coloured arcs on which we put the toll stations. We still have to decide how to arrange them, but this is an easier task than finding a "compatible factor set".

Questions

~~Here are some questions whose answers I would like to know.~~

Starting with prime cyclic groups, and the three operations { ×, ⋊, the addition of toll stations}, can we build all solvable groups?
If the answer to the first question is "yes": starting with all simple groups, and the same three operations, can we build all finite groups?
If the answer to the first question is "no": what is the smallest solvable group that we cannot build this way?

The anser to question 1 is "no".
The answer to question 3 is the group of order 768 generated by (a m i)(b p k)(c n l)(d o j)(f h g) and (a p f l c m h i)(b o e k d n g j): this group can be described as C₂⁵⋊↑S4.
I am grateful to Marston Conder for these answers.

Notation

I shall use the symbol ↑ to indicate a central extension. For example, C4 can be regarded as C2 ↑ C2, and the quaternion group as C2 ↑ (C2 × C2).

In fact any of C4×C2, D8, and Q8 can be represented as C2 ↑ (C2 × C2): see figs. 13, 14, 21, 22 and 23. However C4×C2 and D8 can be built more simply in other ways, so C2 ↑ (C2 × C2) will be taken to denote Q8.


Fig. 57
Two toll stations, pointing opposite ways, on an arc with no arrow


Fig. 56
Two toll stations on an arc with an arrow


Fig. 55
Two toll stations on an arc with no arrow

On other pages I use toll sations in more ways than appear on this page, as shown to the right. I hope their meaning is obvious, but it is specified below.

In Fig. 55, there are two toll stations pointing to the right, and no arrow. The arc can be traversed in either direction. If from left to right, you collect two toll beans; if from right to left, none.

In Fig. 56, there are two toll stations pointing to the right, and an arrow. The arc can only be traversed from left to right, and you collect two toll beans.

In Fig. 57, there are two toll stations, one pointing each way, and no arrow. The arc can be traversed in either direction. Either way, you collect one toll bean.


Fig. 58
(C4×C4) ⋊ C3. Toll stations of two colours in one Cayley diagram.

More than one kind of bean

The "toll bean" notation can be extended to the use of more than one colour, as seen in the diagram to the right.

The two (or more) kinds of bean commute. Picking up an orange bean and then a pink bean is equivalent to picking up an pink bean and then an orange bean.

It may appear that the group portrayed by the diagram to the right should have C2 × C2 in its centre. In fact it does not, its centre has only one element. The orange bean group and the pink bean group are acted on by the period-three elements in a way that leaves neither central.

This is a sub-page of How to build groups.
More pages on groups.